The e.g. 30th birthday is celebrated with more attention than the 27th birthday. Why is this so? The reason is the zero after the three or in mathematical terms the multiple of ten (your daily numeral system with base 10). As a computer affine guy I celebrate the 32nd birthday even more because it has a lot more zeros, at least in the binary, octal, hexadezimal and duotrigesimal (base 32) numeral systems. The small and not so unimportant question appeared.
Which birthday has to be celebrated the most?
This gives me the opportunity to use one of my favorite computation methods: Brute Force. I like to use brute force algorithms because of their simplicity. There are no gradients I have to follow, no clever selection of choices, no neural gas and no discussion about the runtime order because brute force algorithms perform badly. A big plus is, that you scan the whole parameter space without exception.
Now back to the task: Which is the birthday with the most zeros in “all” number systems? Actually I only use the number systems from 2 to 128 because no human according to Wikipedia got older than 122 years and I like numbers, which are two to the power of a natural number.
Lets establish the solution step by step and than perform some induction programming. The idea is to find a simple mathematical rule, which gives us the number of zeros. Lets start with the binary system. The following numbers are interesting for our solution:
| Base 2 Numeral System | Short Decimal Representation | Decimal Representation | Number of Zeros |
|---|---|---|---|
| 10 | $2^1$ | 2 | 1 |
| 100 | $2^2$ | 4 | 2 |
| 1000 | $2^3$ | 8 | 3 |
| 10000 | $2^4$ | 16 | 4 |
| 100000 | $2^5$ | 32 | 5 |
| 1000000 | $2^6$ | 64 | 6 |
| 10000000 | $2^7$ | 128 | 7 |
| 100000000 | $2^8$ | 256 | 8 |
One could assume, to go through each base $b$ with the exponent $e$ and the exponent gives us the number of zeros. This has a caveat which is shown in the following table for the numeral system with base three:
| Base 3 Numeral System | Short Decimal Representation | Decimal Representation | Number of Zeros |
|---|---|---|---|
| 10 | $1 \cdot 3^1$ | 3 | 1 |
| 20 | $2 \cdot 3^1$ | 6 | 1 |
| 100 | $1 \cdot 3^2$ | 9 | 2 |
| 200 | $2 \cdot 3^2$ | 18 | 2 |
| 1000 | $1 \cdot 3^3$ | 27 | 3 |
| 2000 | $2 \cdot 3^3$ | 54 | 3 |
| 10000 | $1 \cdot 3^4$ | 81 | 4 |
| 20000 | $2 \cdot 3^4$ | 162 | 4 |
This looks like a better solution with $n$ from 1 to $b-1$ times $b^e$. The caveat here is, that $110_3$, $120_3$, $210_3$ etc. are missing in the list.
Another problem with the decimal system we live in. It does not explain if we celebrate the $101$ birthday more then the 10th birthday? Lets keep it simple and say: Each zero counts, no matter of its place in the number.
Because the very simple mathematical solutions do not get the results I want, I would have to switch on my brain to figure a clever way to find the solution. Because thinking is difficult, I start programming ;-)
The idea is to represent a year in all number systems from base 2 to base 128 (127 systems) and then to count the zeros. Do this for all years from 0 128. Et Voila. To do this a new Python script is born:
Gist: https://gist.github.com/Threadmonkey/bf07ee6af7134d8b5b90cabe595f3778
As you can guess, birth at year 0 has in ‘all’ numeral systems a zero, which makes it the winner by far. Here a chart with the number of zeros on the y-axis and the years on the x-axis.
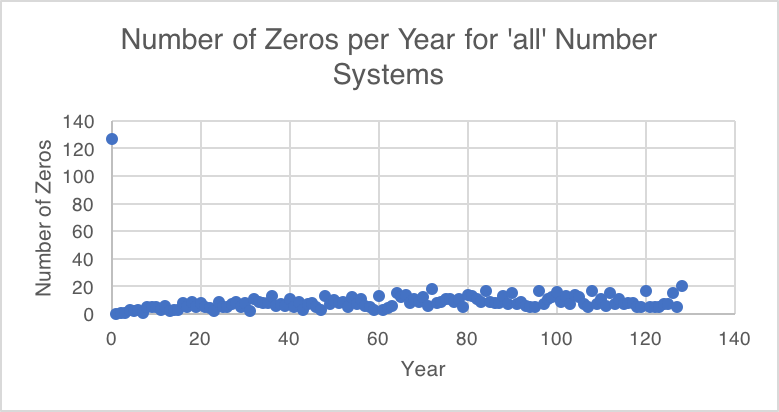
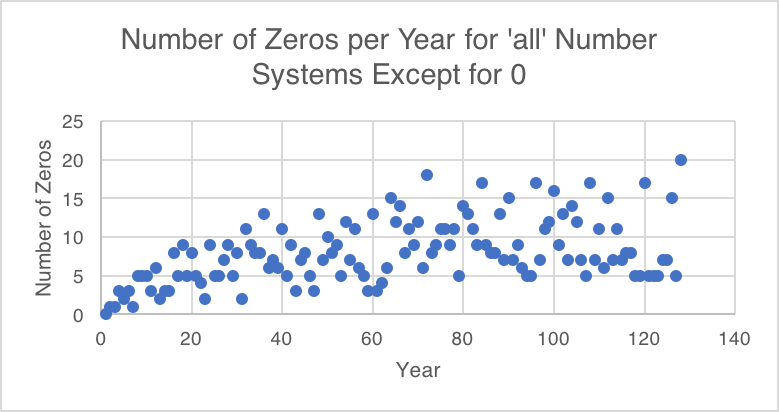
To see a little bit more details, here without the outlier.
Conclusion
- Celebrate your birth as much as you can
- The older you get the better/harder you have to celebrate/party
- The 72nd birthday is the new 50th birthday
- The 72nd birthday is even the new 100th birthday
I hope you had fun reading. If there is a broader interest in this topic, I would invest more time on a more detailed investigation. Let me know.
I have one less 0 in my next birthday from my last. Does that mean I’m supposed to have one less drink? :-(
Hmmm this is a legitm question. I did not find a direct solution (1st page of google search results :-) but some helpful sites:
For party newbies a Drink-calculator
Also for newbiews a small guide:
The-amount-of-booze-you-need-to-drink-to-survive-themed-childrens-birthday-parties
But the solution to your question is still undiscovered and waiting to be found. Give me some time. Maybe there is mathematical relation to the number of drinks and the birthday number.
LOL, Thank you for your research! Actually I may keep the second website as it may come in handy sometime.
As for the question on how many drinks I should have on my next birthday perhaps I’ll have the same as my last or maybe kick it up a notch and have one or two more. We’ll see if I recover as quickly or if it may take a bit longer!
It’s some months away but I’ll let you know my results.